Creating a statistical model

Overview

A formula describes how the columns of your dataset are mapped in the statistical model. For example, the table shows three columns: CO₂ Uptake, Fertilization, and Water Stress. Here, the CO₂ Uptake would be the response variable, i.e., the left side of your model. The variables Fertilization and Water Stress would be the predictors, i.e., the right side of the model. The idea is to see how the predictors affect the response variable. The aim is to see how CO₂ Uptake depends on sufficient Fertilization and Water Stress.

CO2 Uptake	Fertilization	Water Stress
0.01	0.5	yes
0.01	0.5	yes
0.6	0.5	no
0.6	0.5	no
0.3	10	yes
0.2	10	yes
0.01	10	no
0.01	10	no

---

Getting Started

To create your statistical model:

1. Select a variable from the dropdown for the left side of your model.
2. Choose predictor variables from the right side using the buttons provided.
3. Add any necessary arithmetic operations using the operator buttons.
4. Click the Create Statistical Model button to build your model.

Here is an example of a simple model:

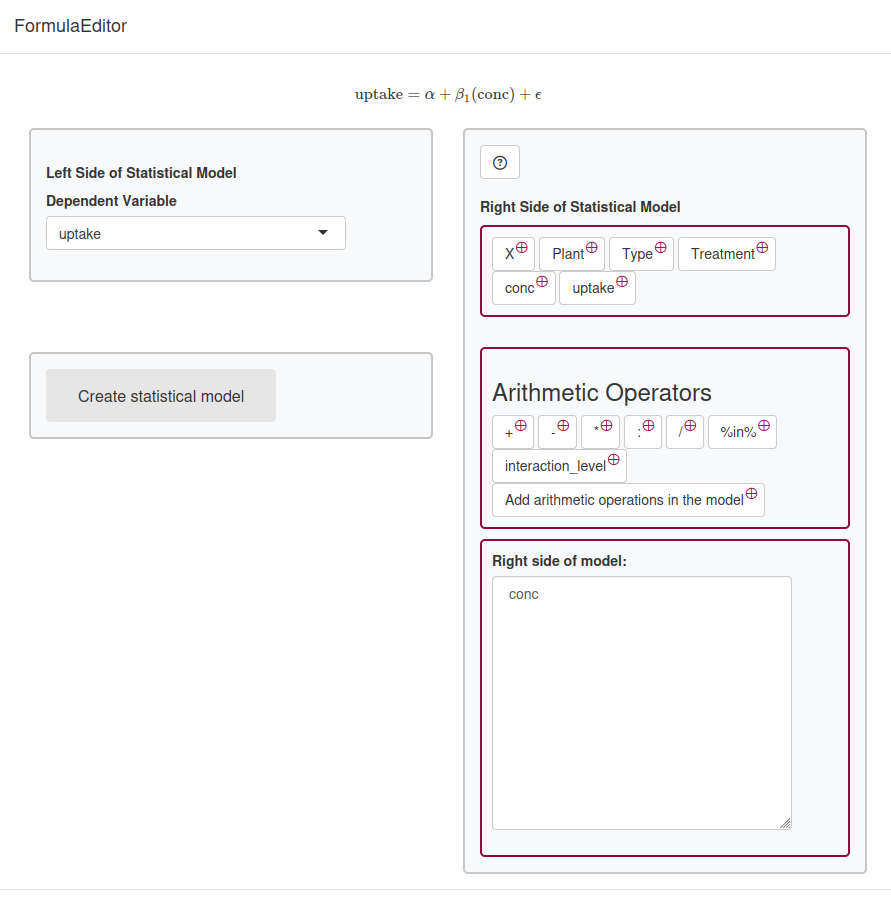
Left Side of the Statistical Model

This section allows you to define the left side of your statistical model, which typically represents the dependent variable (the outcome you want to predict).

Features

• Variable Selection: Use the dropdown menu to choose a variable for your model.
• Create Model Button: Click this button to build the statistical model once you have selected your variables.

---

Right Side of the Statistical Model

The right side represents the independent variables (predictors) that explain the outcome.

Features

• Variable buttons: Displays the selected predictor variables for your model.
• Arithmetic Operators: Use the provided buttons to include mathematical operations between variables. Each operator button serves a specific purpose:
  • Add (+): Include an additional predictor variable.
  • Subtract (-): Remove a predictor variable from the model.
  • Multiply (*): Assess interactions between variables.
  • Colon (:): Include interactions between two variables.
  • Divide (/): Include nested effects that consider both variable levels.
  • Nested (%in%): Include nested effects without including the main level.
  • Interaction Level: Specify the interaction level in the model.
  • Add Arithmetic Operations (I()): Perform normal arithmetic operations within the I() function.
• Editable Code Area: A text area where you can manually edit the right side of the model if needed. This is useful for users who want to refine their formulas directly.

---

Basic Formula with ~

Formula:
weight = α + β₁(height) + ε

height	weight
150	50.71908
160	60.07763
170	70.42381
180	80.13322
190	90.86159

Formula:
weight ~ height

term	estimate	std.error	statistic	p.value
(Intercept)	-100.135956	2.1344248	-46.91473	2.13e-05
height	1.003406	0.0125122	80.19408	4.30e-06

term	ßs	Standard error of ßs	t-statistic = ßs / Standard error of ßs	p.value
Baseline weight (predicted weight if size = 0)	-98.6001595	1.1248337	-87.65755	3.3e-06
Effect of height on weight	0.9944479	0.0065939	150.81351	6.0e-07

---

Adding Multiple Predictors with +

Formula:
price = α + β₁(size) + β₂(bedrooms) + ε

price	size	bedrooms
200.1808	1000	2
250.5359	1500	3
300.0354	2000	3
350.9145	2500	4
400.1657	3000	4

Formula:
price ~ size + bedrooms

term	estimate	std.error	statistic	p.value
(Intercept)	98.7921656	0.4884948	202.237890	0.0000244
size	0.0988738	0.0003674	269.119270	0.0000138
bedrooms	1.1958461	0.3471582	3.444672	0.0749271

term	ßs	Standard error of ßs	t-statistic = ßs / Standard error of ßs	p.value
Baseline price (for size = 0, bedrooms = 0)	98.7921656	0.4884948	202.237890	0.0000244
Effect of size on price	0.0988738	0.0003674	269.119270	0.0000138
Effect of bedrooms on price	1.1958461	0.3471582	3.444672	0.0749271

• Add size and bedrooms as main effects
• A main effect means that the factor is modeled independently from other factors.

---

Model with Main Effects and Interaction Using *

Formula:
yield = α + β₁(fertilizer_Low) + β₂(water_Low) + β₃(fertilizer_Low x water_Low) + ε

yield	fertilizer	water
80	High	High
55	High	Low
77	High	High
56	High	Low
35	Low	High
40	Low	Low
48	Low	High
53	Low	Low

Formula:
yield ~ fertilizer * water

term	estimate	std.error	statistic	p.value
(Intercept)	78.5	4.663690	16.832167	0.0000730
fertilizerLow	-37.0	6.595453	-5.609926	0.0049602
waterLow	-20.0	6.595453	-3.027830	0.0054674